charting – Coffee Spoons

No Matter What You Say, I’m Still Me

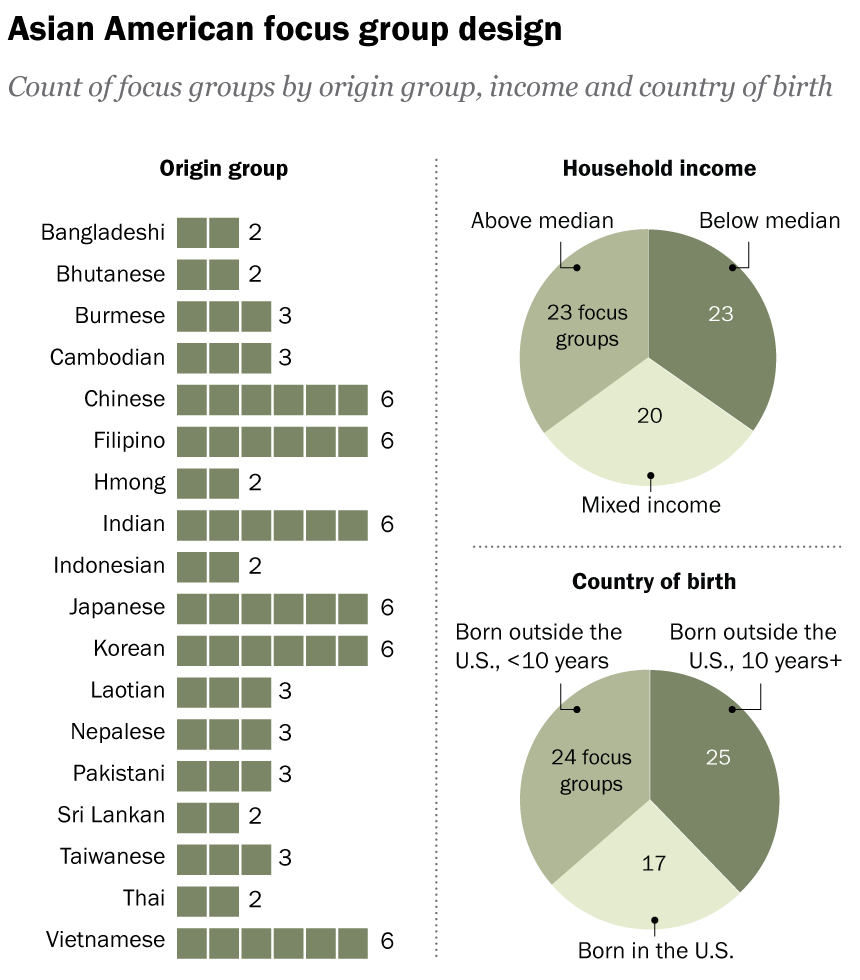
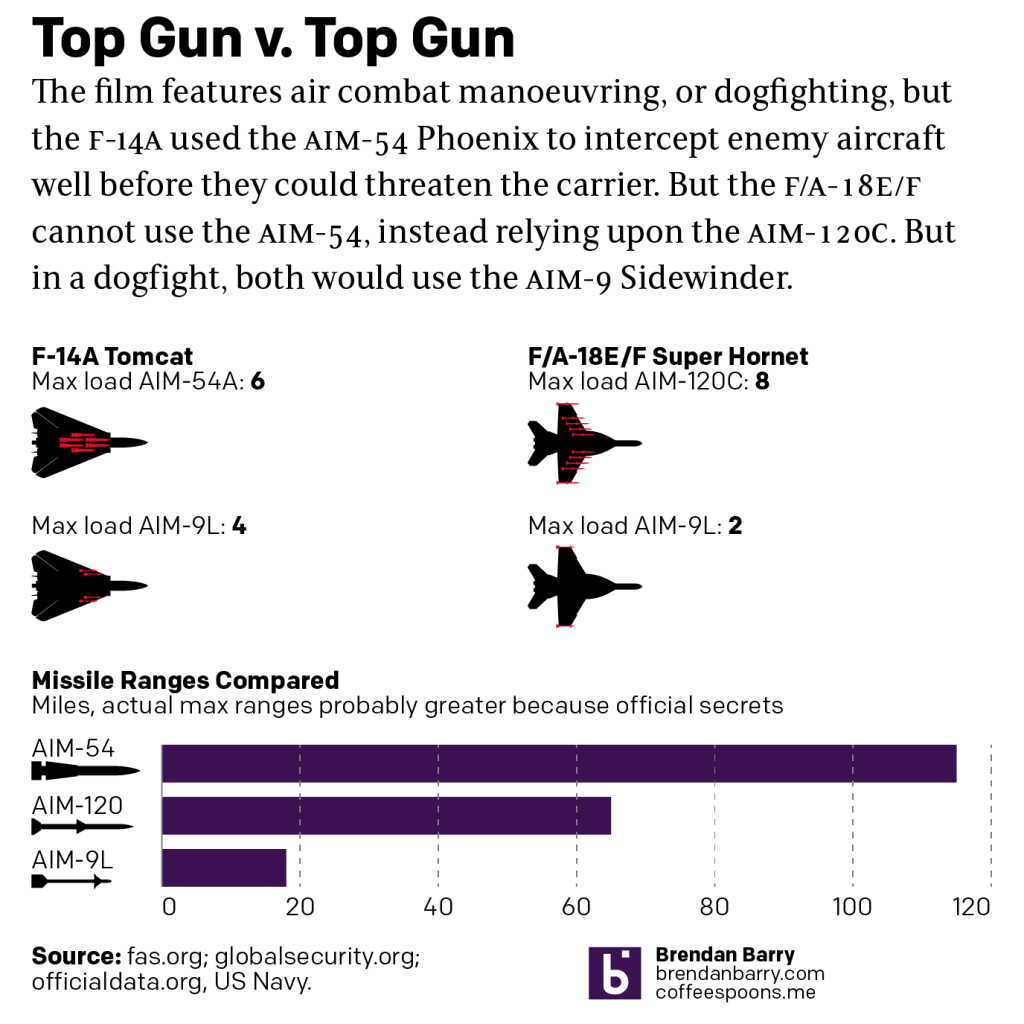
As many long-time readers know, I was long ago bitten by the genealogy bug and that included me taking several DNA tests. The real value remains in the genetic matches, less so the ethnicity estimates. But the estimates are fun, I’ll give you that. Every so often the companies update their analysis of the DNA and you will see your ethnicity results change. I wrote about this last year. Well yesterday I received an e-mail that this year’s updates were released.

So you get another graphic.

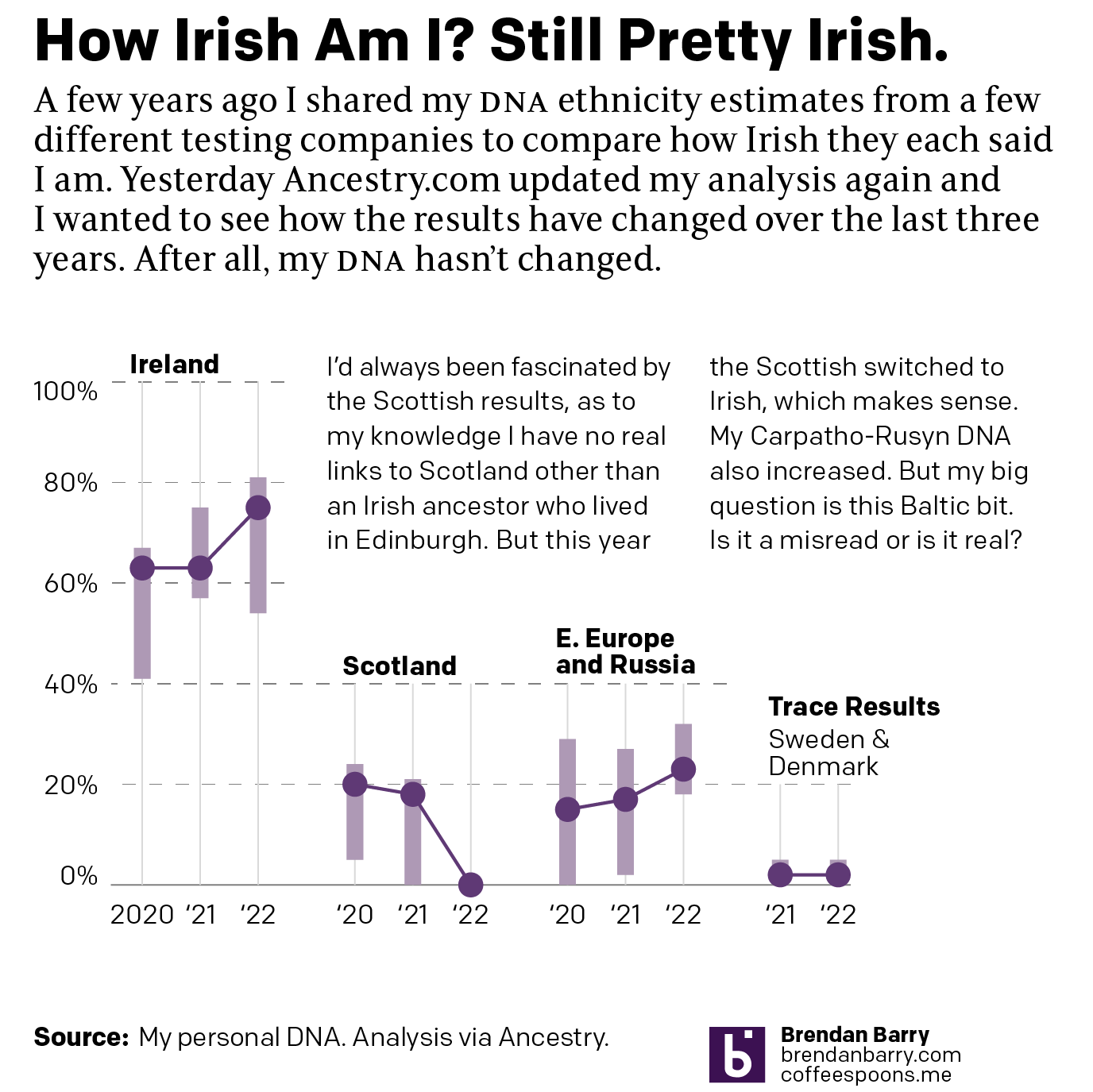
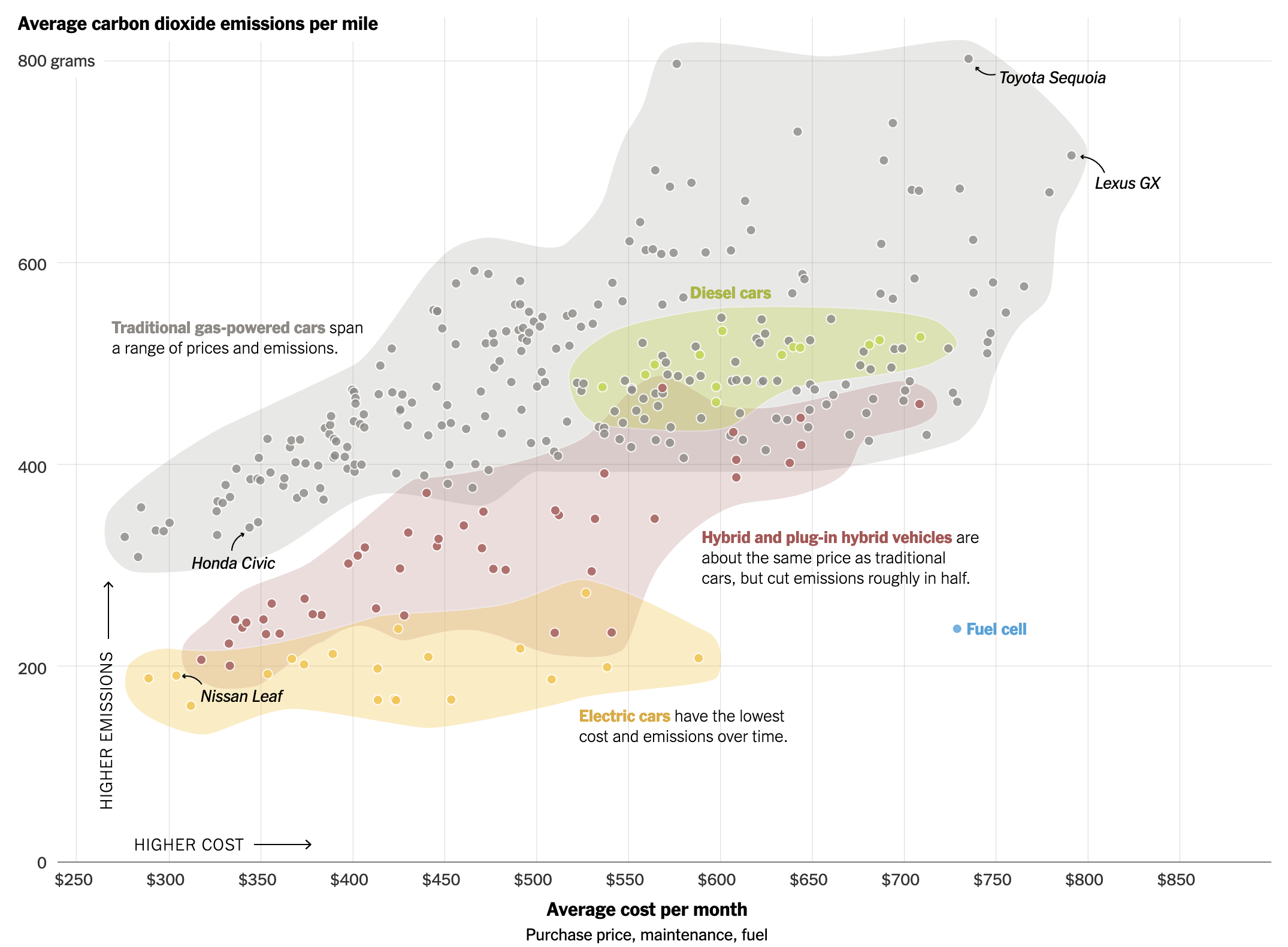
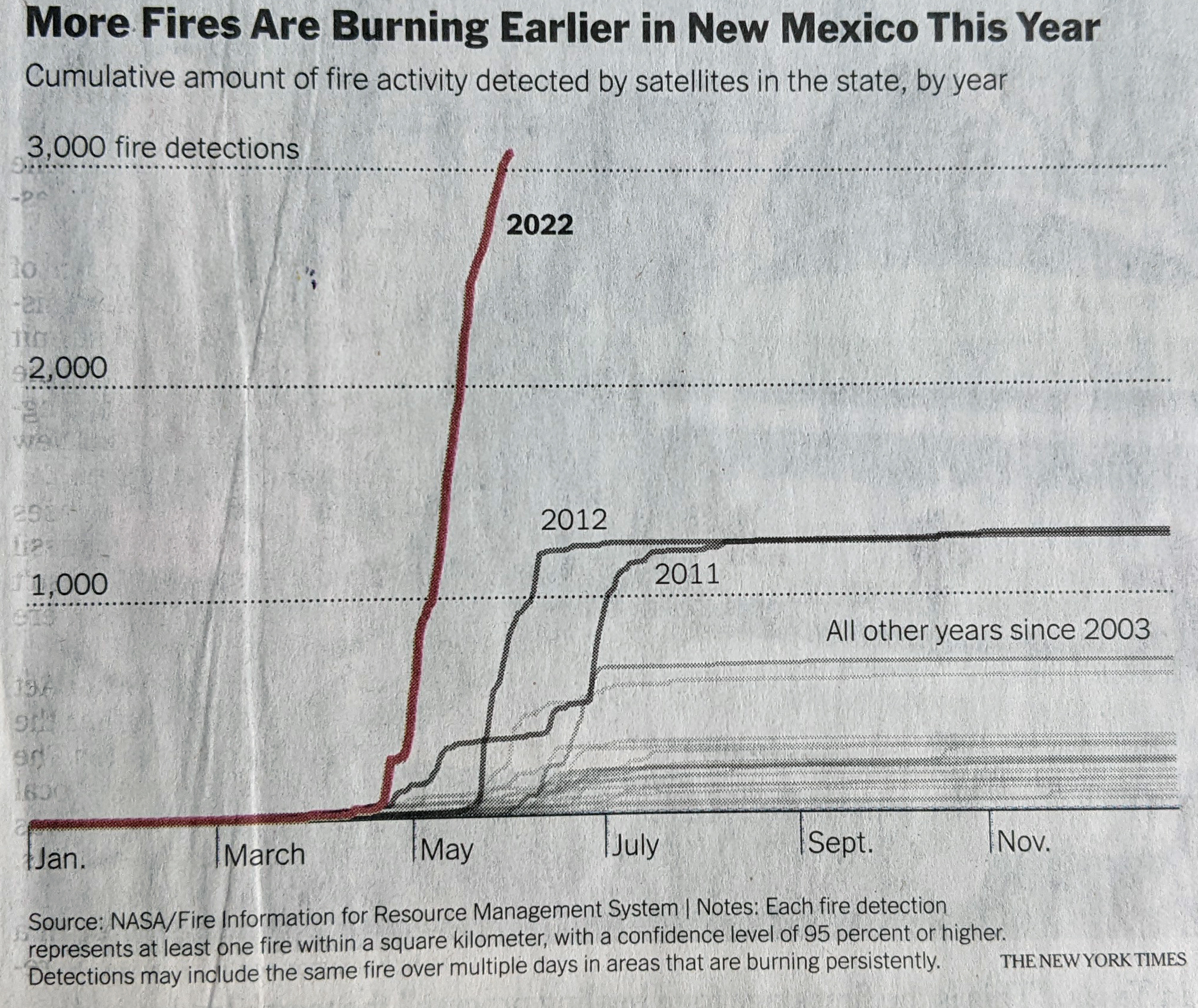
The clearest change is that the Scottish bit has disappeared. How do you go from nearly 20% Scottish to 0%? Because population groups in the British isles have mixed for centuries. When the Scottish colonised northern Ireland, they brought Scottish DNA with them. And as I am fairly certain that I have Irish ancestors from present-day Northern Ireland, it would make sense that my DNA could read as Scottish. But clearly with the latest analysis, Ancestry is able to better point to that bit as Irish instead of Scottish. And this shouldn’t surprise you or me, because those purple bars represent their confidence bands. I might have been 20% Scottish, but I also could have been reasonably 0% Scottish.

Contrast that to the Carpatho-Rusyn, identified here as Eastern European and Russian. That hovers around 20%, which makes sense because my maternal grandfather was 100% Carpatho-Rusyn—his mother was born in the old country, present-day Slovakia. We inherit 50% of our DNA from each of our parents, but because they also inherit 50%, we don’t necessarily inherit exactly 25% from our grandparents and 12.5% from our great-grandparents, &c.

But also note how the confidence band for my Carpatho-Rusyn side has narrowed considerably over the last three years. As Ancestry.com has collected more samples, they’re better able to identify that type of DNA as Carpatho-Rusyn.

Finally we have the trace results. Often these are misreads. A tiny bit of DNA may look like something else. Often these come and go each year with each update. But the Sweden and Denmark bit persisted this year with the exact same values. If I compare my matches, my paternal side almost always has some Swedish and Danish ethnicity, not so for my maternal side. And importantly, those matches have more. Remember, because of that inheritance my matches further up on my tree should have more DNA, and that holds true.

That leads me to believe this likely isn’t a misread, but rather is an indication that I probably have an ancestor who was from what today we call Sweden or Denmark. Could be. Maybe. But at 2%, assuming the DNA all came from one person, it’s probably a 4th to a 6th great-grandparent depending on how much I and my direct ancestors inherited.

Clearly there’s more work to do.

Climate Conscientious and Cheaper Cars

Sometimes in the course of my work I stumble across graphics and work that I previously missed. In this case I was seeking a post about one of my favourite infographics, but it turned out I’ve never posted about it and so I will have to rectify that someday. However in my searching, I came upon an article from the New York Times last year where they wrote about research from MIT that compared the carbon dioxide emissions—bad for the environment and climate—per mile to the average monthly cost of a wide range of 2021 vehicles. The important distinction here is that average monthly cost is not the sticker price of a vehicle, but rather the sticker price plus lifetime operating costs. (For their analysis, the authors assumed a 15-year lifespan and 13,000 miles driven per year.)

Why is this so important? It’s pretty simple, really. In the United States, vehicle emissions are the largest source of carbon emissions. And the vast majority of that is due to passenger vehicles. If we as a society want to get serious about reducing our carbon footprint, the biggest changes we need to make are reducing our amount of driving, moving more people into mass transit, or switching out people’s gas-powered vehicles for electric vehicles.

The New York Times turned their work into a really nice static datagraphic. It is static, so there is no real interactivity if you want to compare your vehicle to others. However, the designers did choose some popular models and identified some of the key outliers.

There are nice annotations here that double their effort as a legend here.

The designers group the cars, represented by dots, into colour fields. These do a good job of showing how there is overlap between the different types of vehicles. Not all hybrid and plug-in vehicles are cheaper or even less CO2 emitting than some gas-powered vehicles, typically your smaller compacts and hatchbacks. Each colour field is linked to a textual annotation that also functions as a legend.

That alone is very helpful in understanding the differences, subtle and not-so-much, between the types of vehicles. Later on in the article the designers also used a scatter plot of a narrower set of data to compare a select set of vehicles.

Here we can see that one cannot simply assume that all electric vehicles are cheaper long-term than their gas-powered compatriots. Here we can see that the Nissan Altima, whilst emitting more CO2, compares favourably with the Tesla Model 3 in both the long-term cost but also in the upfront sticker price.

Despite finding this article a year and a half late, we can tie this to current events in that President Biden’s climate bill creates tax credits for electric vehicles. While the bill is perhaps not as significant as many would like, it is remarkable for still being a lot of money devoted to reducing our emissions. And when it comes to electric vehicles, one of the key components is the creation of tax credits. These would help mitigate those upfront sticker costs of electric vehicles. Because whilst they may generally be cheaper in the long-run, you still need to put up more money than their conventionally-powered alternatives either as lump sums or down payments. And with interest rates rising, what you need to cover via an auto loan will become more expensive.

Overall this is a really nice piece. Should I ever need to buy another vehicle, I would love to see this as a resource available to the general public. Unfortunately it only compares 2021 vehicles. And it does make me wonder where my 2005 vehicle compares. Probably not too terribly favourably.

Credit for the piece goes to Veronica Penney.

Just Keep Grinding it Out

There are certain journalism outlets that I read that consistently do a good job with information design or at least are known for it. Now I try to keep my media diet fairly large and ideologically broad, but in that there are also still some outlets that feature quality design than others. The New York Times, the Washington Post, and the Economist are usually probably top of my list, but you will also see the Wall Street Journal, Philadelphia Inquirer, Boston Globe, the Guardian, and the BBC. I also read more niche outlets for some of my interests, e.g. the Athletic for Red Sox and baseball. But these often don’t feature information design. Politico is one that I read for my political news fix. And when I was reading it whilst on holiday, I was surprised to find an article about the employment market with a really nice line chart.

The article examines the changing labour market where, for over a year now, bargaining power largely resided with employees. If employees wanted raises, benefits, perks, whatever, they could often leave their current employer if their requests weren’t met because another employer, desperate for staff, would likely meet their asks. However, as the economy cools, we would expect the labour market to tighten making few openings available. That begins to reduce the bargaining power of employees as now employers can say “take it or leave it”, knowing that the offers they make to staff aren’t likely to be met by other employers who don’t have open positions or aren’t otherwise hiring.

Four graphics punctuate the article, detailing just that changeover. The full article is worth a read, but I wanted to take a look at one graphic that I think best captures the design decisions made.

That looks like an inflection point to me.

My screenshot above doesn’t capture the interactivity, but we will return to that in a moment. We see three data series: job openings, quits, and layoffs and discharges. The designer represented each with a primary colour, making clear distinctions between the three, and since all three are represented by thousands of units, they can be plotted together. That allows one to make easy comparisons across the three series at particular moments in time, e.g. the Covid recession. My only real quibble is with that recession bar. I probably would have used a neutral colour like a light grey instead of red, because the red appears visually linked to layoffs and discharges when they really are not.

Normally when we see an interactive line chart, we have a small legend above, sometimes below, the graphic. Here, however, the labelling for the lines sit directly next to the line. This makes the display clearer for the reader who scans the data series and I’ve seen the approach often in print, but rarely for interactive work.

And when the reader mouses over the work, the highlight does a few nice things.

We can first see that the line with which the user is engaged becomes the focus: the remaining two lines recede into the background as they are greyed out. We also get a simple, but well designed text label above the cursor. Note how that behind the text there is a thin white stroke that creates visual separation between the letters and the data line. And that cursor is a small grey circle surrounding the data point, allowing you to see said data point.

Take it all together and you have a very clear and very effective interactive line chart. It’s a job well done.

When I see good work from unexpected places it’s important to call it out and highlight it because it means some design director somewhere cares enough to try and improve their publication’s quality of communication. And in an era when many outlets suffer from disinvestment and cost-cutting staff reductions that leave fewer designers, editors, and photographers on staff it is easy to imagine design quality decreasing.

So credit for this piece goes to Eleanor Mueller.

Facebook’s for the Old Folks

We start this work week with something that the young people use, but in a different way than older people do, including elder millennials like myself: social media. Of course, as an elder millennial, I remember Facebook when it was The Facebook when it expanded access to Penn State, which I attended for a single year.

Pew Research conducted a study of teenagers that revealed they use social media more than ever before, but that they use new (sort of) platforms more than the venerable paragon of the past: Facebook.

The Economist’s Data Team looked at the data and created this graphic showing the trends.

We see stacked bar charts on the left and then a line chart on the right. The left-hand chart shows the frequency with which teenagers use various social media platforms. What I don’t understand is how someone uses a social media application “almost constantly”. But that’s probably why I’m an elder millennial.

Get off my lawn, you whippersnappers.

On the right we see the percentage of teenagers who have used an application at least once. The biggest winners? Applications primarily featuring image over text. The losers? Those that use words.

Now longtime readers know that I am not terribly fond of stacked bar charts, especially because they make comparisons between, in this case, social media platforms very difficult. And I feel like we have a story in the occasional use responses, but it’s tough teasing it out from this graphic.

On the right, well, this is one I enjoy. You can tell just how much the social media environment has evolved in the last 7–8 years because TikTok did not exist and YouTube was not thought of as a social media platform.

I wonder if different colours were truly needed for the line chart. The lines do not really overlap and there is sufficient separation that each line can be read cleanly. If the designers wanted to highlight the fall of Facebook or another story line, they could have used accent colours.

But overall a solid graphic.

Now to check my feeds.

Credit for the piece goes to the Economist’s Data Team.

What It Is to be Asian American

Pew recently released a report into the Asian American experience. The report used 66 different focus groups to gather feedback and then summarised that with quotes, video bits, and lots of text. But at the beginning of the report was a nice little graphic that detailed the composition of the focus groups.

This is not a fancy graphic, nor need it be given its supplemental role to the overall piece. But I think it does a reasonable job of showing the construction of the overall focus group demographics, a key point to understanding the responses.

On the left we have a simple count of the number of focus groups by origin. For Indonesians we see there were two focus groups. And thus we have a number two besides the two blocks. Here the two is entirely extraneous and serves as a distracting visual sparkle at the end of the blocks. The advantage of using blocks as opposed to say a bar is that you can visualise the individual components or units, in this case there were two distinct focus groups of Indonesian origin. A user reading this chart should be able to count two blocks. And if they cannot count two blocks, I suspect they would be unable to grasp what the “2” means let alone the rest of the report.

To the right we have two pie charts. My…reticence…to use pies is well-known to long-time readers of Coffeespoons. But here we have the same type of data, counts of focus groups, and I have to wonder: why the designers did not stick with the same model of using individual blocks?

Here I chose to redesign the pie charts.

Nothing here is really new, I just removed the labels because people can count if they need to know the exact number. The labels add visual clutter to the design. And then of course I removed the pie charts and replaced them with blocks like on the left. I was even able to keep the layout roughly the same, albeit within my own graphics template.

Credit for the original goes to the Pew graphics department.

Credit for the redesign is mine.

The Great British Baking

Recently the United Kingdom baked in a significant heatwave. With climate change being a real thing, an extreme heat event in the summer is not terribly surprising. Also not surprisingly, the BBC posted an article about the impact of climate change.

The article itself was not about the heatwave, but rather the increasing rate of sea level rise in response to climate change. But about halfway down the article the author included this graphic.

As graphics go, it is not particularly fancy—a dot plot with ten points labelled. But what this piece does well is using a dot plot instead of the more common bar chart. I most typically see two types of charts when plotting “hottest days” or something similar. The first is usually a simple timeline with a dot or tick indicating when the event occurred. Second, I will sometimes see a bar chart with the hottest days presented all as bars, usually not in the proper time sequence, i.e. clustered bar next to bar next to bar.

My issue with the the latter is always where is the designer placing the bottom of the bar? When we look at the best temperature graphics, we usually refer to box plots wherein the bar is aligned to the day and then top of the bar is the daily high and the bottom of the bar the daily low. It does not make sense to plot temperatures starting at, say 0º.

In this particular case, however, the dates would appear to overlap too closely to allow a proper box plot. Though I suspect—and would be curious to see—if the daily minimum temperatures on each of those ten hottest days have also increased in temperature.

As to the timeline option, this does a better job of showing not just the increasing frequency of the hottest days, but also the rising maximum value. In the early 20th century the hottest day was 36.7ºC, and you can see a definite trend towards the hottest days nearing and finally surpassing 40ºC.

I do wonder if a benchmark line could have been added to the chart, e.g. the summertime average daily high or something similar. Or perhaps a line showing each day’s temperature faintly in the background.

Finally, I want to point out the labelling. Here the designers do a nice job of adding a white stroke or outline to the outside of the text labels. This allows the text to sit atop the y-axis lines and not have the lines interfere with the text’s legibility. That’s always a nice feature to see.

Credit for the piece goes to the BBC graphics department.

Warming Towards Women Leaders

We are going to start this week off with a nice small multiple graphic that explores the reducing resistance to women in positions of leadership in Arab countries. The graphic comes from a BBC article published last week.

These kinds of graphics allow a reader to quickly compare the trajectory of a thing between a start and an endpoint. The drawback is it can obscure any curious or interesting trends in the midpoints. For example, with Libya, is its flat trajectory always been flat? You could imagine a steep fall off but then rapid climb back up. That would be a story worth telling, but a story obscured by this type of graphic.

I do think the graphic could use a few tweaks to help improve the data clarity. The biggest change? I would work to improve the vertical scale, i.e. stretch each chart taller. Since we care about the drop in opposition to women leaders, let’s emphasise that part of the graphic. There could be space constraints for the graphic, but that said, it looks like some of the spacing between chart header and chart could be reduced. And I think for most of the charts except for the first, the year range could be added as a data definition to the graphic and removed from each chart. Similar to how every row only once uses the vertical axis labels.

Another way this could be done is by reducing the horizontal width of each chart in an attempt to squeeze the nine from three rows down to two. That would mean two additional chart positions per row. Tight fit? Probably, but there is also some extraneous space to the right and left of each chart and a large gap between the charts themselves. This all appears to be due to those aforementioned x-axis labels. An additional benefit to reducing the horizontal dimensions of each chart is it increases the vertical depth of the chart as each line’s slope, its rise over run, sees its horizontal distance shrink.

Overall this is a really smart graphic that works well, but with a few extra tweaks could take it to the next level.

Credit for the piece goes to the BBC graphics department.

New Mexico Burns

Editor’s note: I was having some technical issues last week. This was supposed to post last week.

Editor’s note two: This was supposed to go up on Monday. Still didn’t. Third time’s the charm?

Yesterday I wrote about a piece from the New York Times that arrived on my doorstep Saturday morning. Well a few mornings earlier I opened the door and found this front page: a map of the western United States highlighting the state of New Mexico.

That doesn’t exactly look like a climate I’d enjoy.

Unlike the graphic we looked at yesterday, this graphic stretched down the page and below the fold, not by much, but still notably. The maps are good and the green–red spectrum passes the colour blind test. How the designer chose to highlight New Mexico is subtle, but well done. As the temperature and precipitation push towards the extreme, the colours intensify and call attention to those areas.

Also unlike the graphic we looked at yesterday, this piece contained some additional graphics on the inside pages.

Definitely not a place where I want to be.

These are also nicely done. Starting with the line chart at the bottom of the page, we can contrast this to some of the charts we looked at yesterday.

Here the designer used axis lines and scales to clearly indicate the scale of New Mexico’s wildfire problem. Not only can you see that the number of fires detected has spiked far above than the number in the previous years back to 2003. And not only is the number greater, the speed at which they’ve occurred is noticeably faster than most years. The designer also chose to highlight the year in question and then add secondary importance to two other bad years, 2011 and 2012.

The other graphics are also maps like on the front page. The first was a locator map that pointed out where the fires in question occurred. Including one isn’t much of a surprise, but what this does really nicely is show the scale of these fires. They are not an insignificant amount of area in the state.

Pointing out where I really don’t want to be in New Mexico.

Finally we have the main graphic of the piece, which is a map of the spread of the Calf Canyon and Hermits Peak fire, which was two separate fires until they merged into one. The article does a good job explaining how part of the fire was actually intentionally set as part of a controlled burn. It just became a bit uncontrolled shortly thereafter.

This reminded me of a piece I wrote about last autumn when the volcano erupted on La Palma. In that I looked at an article from the BBC covering the spread of the lava as it headed towards the coast. In that case darker colours indicated the earlier time periods. Here the Times reversed that and used the darker reds to indicate more recent fire activity.

Overall the article does a really nice job showing just what kind of problems New Mexico faces not just now from today’s environmental conditions, but also in the future from the effects of climate change.

Credit for the piece goes to Guilbert Gates, Nadja Popovich, and Tim Wallace.

Top Gun

Last night I went to see Top Gun: Maverick, the sequel to the 1986 film Top Gun. Don’t worry, no spoilers here. But for those that don’t know, the first film starred Tom Cruise as a naval aviator, pilot, who flew around in F-14 Tomcats learning to become an expert dogfighter. Top Gun is the name of an actual school that instructs US Navy pilots.

Back in the 1980s, the F-14 was the premiere fighter jet used by the Navy. But the Navy retired the aircraft in 2006 and it’s been replaced by the F/A-18E/F Super Hornet, a larger and more powerful version of the F/A-18 Hornet. So no surprise that the new film features Super Hornets instead of Tomcats.

And so I wanted to compare the two.

The important thing to note is that the Tomcat flies farther and faster than the Hornet. The F-14 was designed to intercept Soviet bombers that were equipped with long-range missiles that could sink US carriers. The Hornet was designed more of an all-purpose aircraft. It can shoot down enemy planes, but it can also bomb targets on the ground. That’s the “/A” in the designation F/A-18. In the role of intercepting enemy aircraft, the F-14 was superior. It could fly well past two-times the speed of sound and it could fly combat missions over 500 miles away from its carrier.

In the interception role, however, the F-14 had another crucial advantage: the AIM-54 Phoenix missile. It was a long-range air-t0-air missile designed for the Tomcat. It does not work with any other US aircraft and so the Hornet uses the newer AIM-120 AMRAAM, a medium-range air-to-air missile.

There are plans to design a long-range version of the AIM-120, but it doesn’t exist yet and so the Hornet ultimately flies slower, less distance, and cannot engage targets at longer ranges.

However, dogfighting isn’t about long-range engagements with missiles. It’s about close-up twisting and turning to evade short-range missiles and gunfire. And even in that, the F-14 could use four AIM-9 Sidewinder missiles whereas the F/A-18 carries only two on its wingtips.

By the 2000s F-14 was an older aircraft and while the moving, sweeping wings look cool, they cause maintenance problems. They were expensive to maintain and troublesome to keep in the air. But they are arguably superior to what the Navy flies today.

Moving forward, the Navy is beginning to introduce the F-35 Lightning II to the carrier fleets. Maybe I’ll need to a comparison between those three.

Credit for the piece is mine.

May Jobs Report

Friday the Bureau of Labour Statistics published the data on the jobs facet of the American economy. Saturday morning I woke up and found the latest New York Times visualisation of said jobs report waiting for me at my door. The graphic sat\s above the fold and visually led the morning paper.

We have a fairly simple piece here, in a good way. Two sections comprise the graphic. The first uses a stacked bar chart to detail the months wherein the US economy lost jobs during the previous two and a half years. We can take a closer look in this second photo that I took.

But the recovery hasn’t been uniformly good for all.

Here we can see the stacked bars pile up with the most recent bars to the right. Some of the larger bars have labels stating the number of jobs either lost (top) or gained (bottom). I’m not normally a fan of stacked bar charts, because they don’t allow a reader to easily discern like-for-like changes. In this instance, the goal is to show how close all the little bits have come towards making up the three negative bars. Where I take issue is that I would prefer the designers used some sort of scale to indicate even a rough sense of how many jobs the various bars represent.

That issue crops up again to a slightly lesser degree with the bottom set of graphics. These compare the growth of hourly earnings and inflation both from February 2020. During the first few months of the pandemic and its recession, you can see earnings for those most directly impacted by shutdowns drop. But there is no negative scale accompanying the positive scale and that makes it difficult to determine just how far earnings fell for those in, say, leisure and hospitality.

The second part of the graphic works overall, however it’s just some of the finer design details that are missing and take away from the graphic’s overall effectiveness.

This all fits part of a larger trend in data visualisation that I’ve been noticing the last few months. Fewer charts seem to be using axes and scales. It’s not a good thing for the field. Maybe some other day I’ll write some things about it.

For this piece, though, we have an overall solid effort. Some different design decisions could have made the piece clearer and more effective, but it still does the job.

Credit for the piece goes to Ben Casselman, Ella Koeze, and Bill Marsh.